Multilevel Analysis with Few Clusters: Improving Likelihood-based Methods
- Elff, Martin, Jan Paul Heisig, Merlin Schaeffer, and Susumu Shikano. 2021. “Multilevel Analysis with Few Clusters: Improving Likelihood-based Methods to Provide Unbiased Estimates and Accurate Inference”. British Journal of Political Science 51(1): 412-426. DOI:
10.1017/S0007123419000097
- Abstract:
-
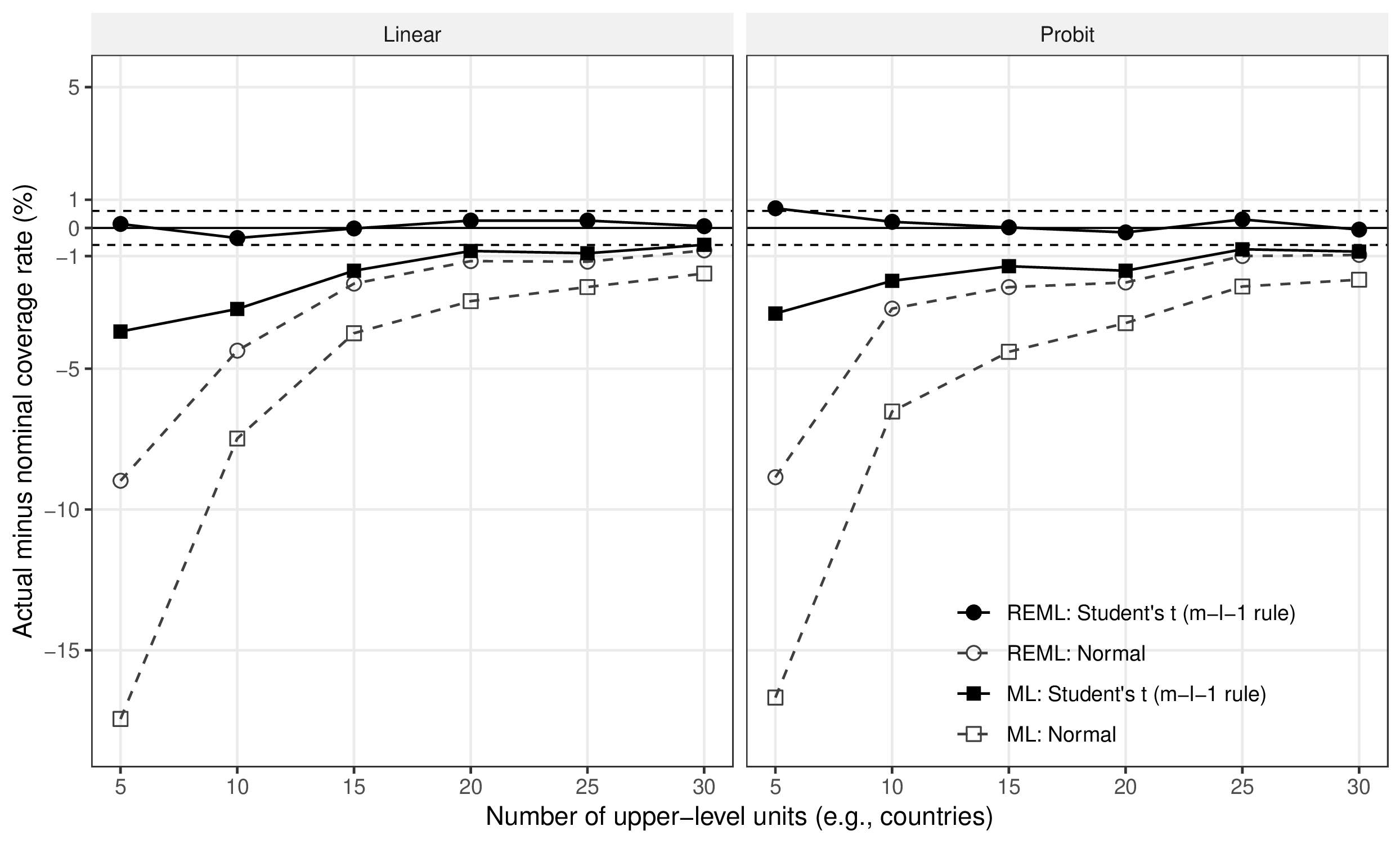
Quantitative comparative social scientists have long worried about the performance of multilevel models when the number of upper-level units is small. Adding to these concerns, an influential Monte Carlo study by Stegmüller (2013) suggests that standard maximum likelihood methods yield biased point estimates and severely anti-conservative inference with few upper-level units. In this paper, we seek to rectify this negative assessment. First, we show that maximum likelihood estimators of coefficients are unbiased in linear multilevel models. The apparent bias in coefficient estimates found by Stegmueller can be attributed to Monte Carlo Error and a flaw in the design of his simulation study. Second, we show how inferential problems can be overcome by using restricted maximum likelihood estimators for variance parameters and a t-distribution with appropriate degrees of freedom for statistical inference. Thus, accurate multilevel analysis is possible within the framework that most practitioners are familiar with, even if there are only a few upper-level units.
View open access article (local copy)
View online appendix (local copy)
Supplementary material (local copies)
- Replication material
- Example application
- R package for improved inference: iimm